はじめに

遅れながらも今年のyoshi-campがやってきました。今回はyoshi-camp in 東北ということで、福島県会津若松市で開催され、@kymn_, @meowricator, @y05h1k1ng, @ptrYudai, @theoremoonの5人が参加しました。

yoshi-campってなぁに？

yoshi-campとは「yoshikingのyoshikingによるyoshikingのための勉強会」です。2年前くらいから半年に1回くらいのペースで日本の各地で開催されています。 yoshi-campは、昔yoshikingがセキュリティキャンプに応募して落ちたことを受けて、セキュリティキャンプより高難易度高品質の勉強会を開こうというモチベーションで生まれたという歴史的経緯があります。慣例的に参加者は全員*1が2時間〜5時間以上の演習付き講義をする必要があり、内容は発表者の自由ですが、他の参加者からのリクエストあるいは自分が勉強したいと思うことをテーマに深く扱います。これまで

LLL, Coppersmith
Forensics + Malware解析
楕円曲線暗号
angr
Z3

などが扱われてきました。

東山温泉街と会場

会津若松駅からタクシーで15分、源泉かけ流しの温泉付き旅館が立ち並ぶ東山温泉街があります。会場はkeymoon-universityの部活が保有している勉強会用スペースを借りました。まだ誰も使ったことがなかったらしいです。

おもしろポイント：

バスが1〜2時間に1本
電車も1時間に1本
初日はバスに失敗して会場まで歩いて1時間
なんかバスの音声案内が壊れてる(?)とのことで運転手が代役
呉服屋っぽい会場
部屋の床がすのこで隙間が大きいので引っかかって足が折れる

1-1: AESに対するサイドチャネル攻撃

初日は我らがyoshikingの講義で、内容は相関電力解析攻撃でした。内容は理解したつもりだけど実装が追いついてないので、この講義のwriteupは他の人に任せます。

解説スライドにAESの図が入っていたのですが、実はこれが若干間違った図になっているというトラップで、事前課題のAES内部構造をちゃんと予習していない人は全員脱落するというスパルタ講師のyoshikingならではの仕組みになっていました。私は無事死亡しました。死亡したのでmitsu君と敗北のピザの買い出しに行ったのですが、その間に他の人は問題解けてて泣いちゃった。

1-2: Multivariate Coppersmith Methodのお気持ちと実装

2コマ目はzer0ptsで一番怖い人、theoremoon組長によるMultivariate Coppersmith Methodを実装する講義でした。

前回のyoshi-campでunivariateなcoppersmithは理解したのですが、今回はmultivariateになりました。単変数の場合

$g_{i,j}(x) = N^{m-i}x^{i}f^{i}$
$h_{i}(x) = x^{i} f^{m}$

として剰余の世界から抜け出して方程式を増やしました。実は他変数でもやることは同じで、 $x^{i}$ の部分として、元の次数までで考えられる $x^{i}y^{j}z^{k}\cdots$ の組み合わせを入れれば良いだけです。

LLLで係数を簡約化したとき、多変数の場合は1つの式では方程式を解けません。そのためLLLで複数解を探し、グレブナー基底を用いて方程式を解きます。みなさんご存知(?)Howgrave-Graham's Lemmaは多変数バージョンもあるらしいのですが、なくても（余計なケースが入るだけで）大丈夫だそうです。

例題としてzer0pts CTF 2021で出題されたeasy pseudo randomを解きました。

import itertools

def my_multivariate_small_roots(f, XYZ, m, t=0):
    """
    My first multi-variate small_roots implementation
    Args:
        f: Polynomial
        XYZ: Maximum value of variables
        m: Extended degree
        t: Magic parameter (f^m, xf^m to x^(t-1)f^(m-1))
    """
    N = f.base_ring().cardinality()
    d = f.degree()
    f = f.change_ring(ZZ)
    xyz = f.parent().gens()

    """
    Step 1. 方程式をかさ増しする
    """
    gs = []
    for i in range(m):
        for degs in itertools.product(range(d), repeat=len(xyz)):
            # degsは各変数の次数を持つ：x*z^3-->(1,0,3)
            g_ijk = N^(m-i) * f^i
            for v, deg in zip(xyz, degs):
                # 例えばx^1, y^0, z^3をかけ合わせる
                g_ijk *= v^deg
            # set X*x to x, Y*y to y, and so on
            gs.append(g_ijk(*list(map(lambda a: a[0]*a[1], zip(xyz, XYZ)))))

    for degs in itertools.product([i for i in range(t)], repeat=len(xyz)):
        h_ijk = f^m
        for v, deg in zip(xyz, degs):
            h_ijk *= v^deg
        gs.append(h_ijk(*list(map(lambda a: a[0]*a[1], zip(xyz, XYZ)))))

    """
    Step 2. 格子を錬成する
    """
    def coefficient_matrix(polys):
        # theoremoon's magic
        monomials = set()
        for p in polys:
            monomials = monomials.union(p.monomials())
        monomials = sorted(list(monomials))
        M = matrix(len(polys), len(monomials))
        for i in range(len(polys)):
            m = polys[i].monomials()
            c = polys[i].coefficients()
            for j in range(len(m)):
                M[i, monomials.index(m[j])] = polys[i].monomial_coefficient(
                    m[j]
                )
        return M, monomials
    B, monomials = coefficient_matrix(gs)

    """
    Step 3. LLLで小さい多項式係数を求める
    """
    l = B.LLL()
    polys = []
    for row in l:
        if row.is_zero():
            continue
        # [TODO] Howgrave-Graham's theorem?
        """
        Step 4. 方程式を戻す
        """
        poly = sum(map(lambda a: a[0]*a[1]/a[1](*XYZ),
                       zip(row, monomials)))
        polys.append(poly.change_ring(QQ))
        I = Ideal(polys) # いである。
        if I.dimension() == -1: # 大杉君
            polys.pop(0) # 古い方程式から優先して抹消
        elif I.dimension() == 0:
            for root in I.variety(ring=ZZ):
                root = tuple(int(root[var]) for var in f.variables())
                yield root

# easy pseudo random
nbits = 256
d = 2
k = ceil(nbits * (d / (d + 1))) # 171, nbits-k=85

p = 43343132318542115908109143315552470697591037366597387898555021129243891268321
b = 41626875266611172180637084755555430560267242697294225673939722754126407735314
m = 26949942292579858219052254038266486253954430094782895839375885288766769341049
w0 = 736213423532176860355024979639742034476924805552604
w1 = 453768168211027546342885075363551218230698462688285

w0 = w0 << (nbits - k)
w1 = w1 << (nbits - k)

PR.<x0,x1> = PolynomialRing(GF(p))
f = w0*w0 + 2*x0*w0 + x0*x0 - w1 + b - x1
for r in my_multivariate_small_roots(f, [2**85, 2**85], m=4, t=0):
    y0, y1 = r

    v0 = int(w0 + y0)
    v1 = int(w1 + y1)

    P.<v> = PolynomialRing(Zmod(p))
    F = v^2 + b

    v = v1
    for i in range(5):
        v = F(v)
        m ^^= int(v)
    print(bytes.fromhex(hex(m)[2:]))

実装を永遠にバグらせたので先生にデバッグしてもらいました。なんかグレブナー基底を理解してなかったのが悪かったらしい。

1-3: Linux Kernel Exploit入門

3コマ目は今回のcampで一番簡単なLinux Kernel Exploitの演習です。参加者には脆弱性のあるカーネルドライバを攻撃してもらい、SMAP, SMEP, KPTI, KASLRを1つずつ追加して各種セキュリティ機構の役割や回避法を勉強しました。時間の都合でKASLRは省略しましたが、全員偉いのでSMAP, SMEP, KPTIを回避して権限昇格できていました。

将来的に公開するかもしれないししないかもしれないのですが、現在pwnを勉強するためのWebサイトを作っています。内容はLinux Userland/Kernel, Windows Userland/Kernel, Browser, VMです。一生完成しなさそう。

今回は講義資料としてこのWebサイトのLinux Kernelの部分を利用しました。一生完成しなさそう（二回目）なので一部お披露目しておきます。

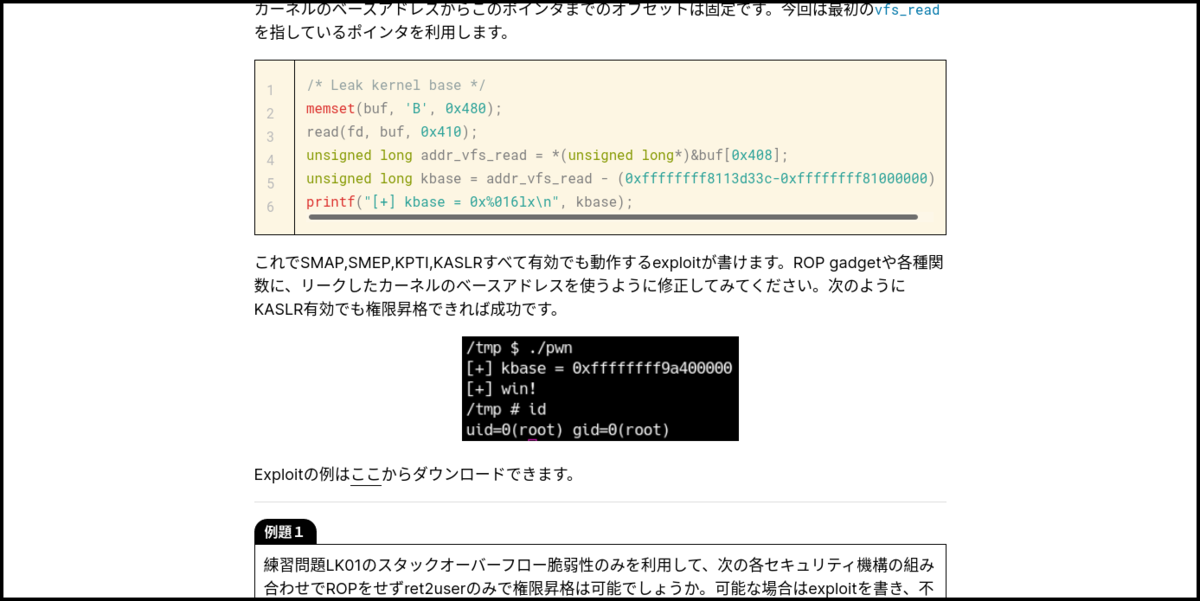
f:id:ptr-yudai:20211117115859p:plain

一生完成しなさそう。（三回目）

2-1: 猫でもわかる超楕円曲線

2日目は真の暗号学者であるmitsu君による超楕円曲線とそれを使った暗号の原理と実装です。楕円曲線の(CTF向け)講義は昔私もやりましたが、今回のはより深く数学的側面から暗号に結びつけるガチ講義でした。

今まで当たり前のように種数1の楕円曲線しか触ってきませんでしたが、今回は種数がより大きい超楕円曲線を勉強しました。まずWeierstrassの $\wp$ 関数のパラメータから生成された格子 $\Lambda$ を考えたとき、 $\mathbb{C}/\Lambda$ と複素トーラス上の点が同型であるという古の知識を復習しました。そう考えると位相幾何における種数の考え方を楕円曲線で使ってるのも自然だよね、という話になります。たまげたなぁ。

f:id:ptr-yudai:20211123114321p:plain — mitsu先生作『singularな猫』

まずは超楕円曲線の標準形のお勉強です。超楕円曲線 $C: v^{2} + h(u)v = f(u)$ について $u\mapsto u, v\mapsto v-h(u)/2$ という変換をします。これで出てくる式

$v^{2} = f(u) + h(u)^{2}/2$

が超楕円曲線の標準形となります。曲線を定義したら点も定義します。基本的には楕円曲線と変わりませんが、反数は $(x, -y-h(x))$ となります。次に座標環、多項式、有理関数について定義しましたが、長くなるので省略します。

その後Weil Pairingでおなじみ因子の話が出てきます。超楕円曲線 $C$ のゼロ因子群を $\mathcal{D}^{0}$ 、主因子群を $\mathcal{D}^{l}$ とするとき、剰余群

$\mathcal{J}_{C}=\mathcal{D}^{0}/\mathcal{D}^{l}$

をヤコビアンと呼びます。令和のヤコビアンことmitsu先生直伝のヤコビアンに一同感動。

この代表元を表現する手法としてMumford表現があります。 Mumford表現に対しては高速な加算アルゴリズムがあるので嬉しいらしい。しかしMumford表現は半被約因子にのみ与えられます。これは、次の条件を満たす因子のことを言います。

$D = \sum m_{i}P_{i} - (\sum m_{i})P_{\infty}$
$P_{i} \neq \tilde{P_{i}} \Rightarrow \forall j\neq i, P_{j}\neq \tilde{P_{i}}$
$P_{i}$ が分岐点ならば $m_i = 1$

1の無限遠点は因子の次数を0にするように減算されています。2はPの反数が存在しないことを言っています。3は分岐点を複数持たないという条件です。ちなみに、必ず $\mathcal{J}_{C}$ の元の代表元として半被約因子を持ってくることができるらしい。これに対してMumford表現は次のように定義できます。

体 $K$ 上の超楕円曲線 $C: F=0$ における半被約因子 $D$ のMumford表現とは、 $U,V\in \bar{K}[X]$ の組 $(U,V)$ のことである。 $U,V$ は $P=(x_{i}, y_{i}), U_{i}=X-x_{i}$ とおいたとき、次を満たすものである。*2

こうしてyoshikingは半被約因子鑑定士になったのであった・・・（完）

これが暗号に使えるか問題なのですが、使えません。なぜなら半被約因子は $\mathcal{J}_{C}$ の元を一意に表現できないからです。そこで被約因子というのが登場します。これは半被約因子について、次数が種数より小さい、すなわち $\deg{U} \lt g$ という条件を付けたものです。

しかし、これでもまだ問題があります。一般に $\bar{K}$ が無限位数なのでヤコビアンも無限位数となってしまい、悲しい結果で終わります。そこでヤコビアンの有限部分群を考えます。現状

$\mathcal{J}_{C}=\{(U,V) \in \bar{K}[X]^{2} | \deg V \lt \deg U \lt g, F - V^{2} \equiv 0 \mod U\}$

でした。*3 これを

$\mathcal{J}_{C}(K) = \{(U,V) \in K[X]^{2}\}$

とします。暗号としては $K=\mathbb{F}_{p}$ などと置きます。あとは超楕円曲線暗号ですが、これは楕円曲線同じく、ヤコビアン上の離散対数問題に基づいて定義できます。最後に超楕円曲線暗号で暗号化・復号するスクリプトを書いて終了〜〜。

私は実装パートが早く終わったのでyoshikingと名誉あるピザの買い出しに行っていたのですが、帰ってきたら他の人がより発展的な話題をしてて泣いちゃった。

2-2: 実践・最短経路問題

最後はkey-全強-moonさんの最短経路問題の講義でした。 keymoon先生は強すぎることが一般に知られているので、前日の夜にみんなで講義資料を予習していました。私は競技プログラミングが苦手でたぶんAtCoderとかやったら灰色から転落する可能性すらあります。今回のShortestPathライブラリの状態遷移の考え方は非常にわかりやすく、競プロっぽい問題を解くことができました。いつかCTFで使えれば良いですが、でもCTFに競プロ要素はあまり入れないで欲しい派。

内容は魔女のお茶会でkeymoonさんが発表していた

qiita.com

と同じです。本人解説がある分若干上位互換かな。だいたい↑に書いてあるので私から書くことはなし。

ptrlibでは便利utilityのPR/提案Issueをお待ちしています。

github.com

おまけ：恐竜王戦

旅館ではzer0pts最強の棋士を決める恐竜王戦が開かれました。*4 自分が関与した対局の戦型はこんな感じでした：

第一局：船囲い急戦(mitsu) vs 四間飛車美濃(ptr)
第二局：右四間飛車(mitsu) vs 四間飛車美濃(ptr)
第三局：四間飛車(mitsu) vs エルモ急戦(ptr)
第四局：四間飛車(theoremoon) vs 居飛車穴熊(ptr)
第五局：右四間飛車左美濃(mitsu) vs 雁木(ptr)
第六局：初期状態歩飛角全成5秒切れ負け*5(yoshiking) vs 標準状態(ptr)

真面目に人間と将棋を指したのは久しぶりで楽しかったです。中盤力しかないので中盤で圧倒的差を付けないと苦しいことになる。

*1:会場を貸してくれる人は実は何もせずに参加可能

*2:いい加減はてなのTeX記法使いにくすぎるから直してくれ

*3:この数式をはてなTeXで正しく表示されるのに3億年かかった。

*4:なんか将棋が無料貸出だったので遊んでただけという説もある

*5:時間切れても指し続けるので切れ負けではない

CTFするぞ

CTF以外のことも書くよ

yoshi-camp 2021 autumn 🍂 参加記